Question

In a time of seconds, a particle moves a distance of meters from its starting point, where .

(a) Find the average velocity between and if: (i) (ii) (iii) Enter the exact answers.

(i) When , the average velocity between and is m/sec.
(ii) When , the average velocity between and is m/sec.
(iii) When , the average velocity between and is m/sec.

(b) Use your answers to part (a) to estimate the instantaneous velocity of the particle at time . Round your estimate to the nearest integer. The instantaneous velocity appears to be m/sec.

Answer 1

a) (i) When h=0.1, the average velocity between and is 12.6 m/sec.

(ii) When h=0.01, the average velocity between and is 12.06 m/sec.

(iii) When h=0.001, the average velocity between and is 12.006 m/sec.

b) The instantaneous velocity appears to be 12 m/sec.

Explanation:

The question is incomplete:

In a time of t seconds, a particle moves a distance of S meters from its starting point, where S=6t^2+4.

(a) Find the average velocity between t=1 and t=1+h if: (i) h=0.1 (ii) h=0.01 (iii) h=0.001. Enter the exact answers.

(b) Use your answers to part (a) to estimate the instantaneous velocity of the particle at time t=1. Round your estimate to the nearest integer.

The average velocity can be expressed as:

`\bar v=(\Delta S)/(\Delta t)=(S(1+h)-S(1))/((1+h)-1)= (S(1+h)-S(1))/(h)`

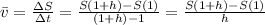
For h=0.1:

`\bar v= (S(1+h)-S(1))/(h)=((6(1+h)^2+4)-(6(1)^2+4))/(h) = (6(1^2+2h+h^2-1^2)+4-4)/(h)\\\\\bar v = (6h(2+h))/(h)=6(h+2)\\\\\\h=0.1\\\\\bar v=6(0.1+2)= 12.6`

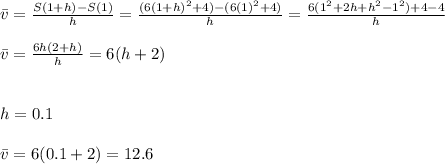
For h=0.01

`h=0.01\\\\\bar v=6(0.01+2)= 12.06`

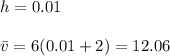
For h=0.001

`h=0.001\\\\\bar v=6(0.001+2)= 12.006`

b) As the h becomes close to zero, the average velocity tends to v=12 m/s