Question

Suppose that X is the number of successes in an experiment with 9 independent trials where the probability of success is 2 5 . Find each of the following probabilities. Round answers to the nearest ten-thousandth.

Answer 1

The complete question is:

Suppose that X is the number of successes in an experiment with 9 independent trials where the probability of success is 2/5 . Find each of the following probabilities. Round answers to the nearest ten-thousandth.

(i) P (X < 2)

(ii) P(X ≥ 2)

Answer:

(i) P(x < 2) = 0.07054

(ii) P(x ≥ 2) = 0.92946

Explanation:

Given that X is the number of successes in an experiment n = 9, and the probability of success p = 2/5

If x is approximated Binomial(n, p)

Then

P(x) = nCxP^xq^(n - x)

Where q = 1 - p

Here, q = 1 - (2/5) = 3/5

And nCx, read as "n combination x"

is given as n!/(n - x)! x!

P(x < a) = P(x = a - 1) + P(x = a - 2) + ... + P(x = 1) + P(x = 0)

And

P(x ≥ a) = 1 - P(x < a)

Now, P(x < 2)

= P(x = 1) + P(x = 0)

= [9C0(2/5)^0 (3/5)^(9 - 0)] + [9C1(2/5)^1 (3/5)^(9 - 1)]

= [1×1×(3/5)^9] + [9 × (2/5) × (3/5)^8]

= 0.070543872

≈ 0.07054 (To the nearest ten thousandth)

Now,

P(x ≥ 2) = 1 - P(x < 2)

= 1 - 0.07054

= 0.92946

Answer 2

Explanation:

The complete is question is as follows

Suppose that X is the number of successes in an experiment with 9 independent trials where the probability of success is 2/5 . Find each of the following probabilities. Round answers to the nearest ten-thousandth.

P (X < 2)

P(X ≥ 2)

Recall that given an event A, we have the following property
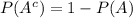`P(A^c)=1-P(A)`. Note that if we consider the event A to be "X<2", its complement is the event "X≥ 2" then, the second probability is

P(X≥ 2) = 1- P(X<2). Therefore, we only need to calculate the first probability to solve the problem.

REcall that given a number of
`n` indepent trials of an experiment whose outcomes are "success" or "fail", where the probability of having a succes is p, the number of success is a random variable that is distributed as a binomial random variable. Therefore, we have that if X is the number of successes,

`P(X=x) = \binom{n}{x} p^x(1-p)^(n-x)`.

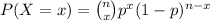In our case, we have that p=2/5 and n=9. Hence,

`P(X<2) = P(X=0) + P(X=1) = \binom{9}{0}(2/5)^0(3/5)^(9-0)+ \binom{9}{0}(2/5)^1(3/5)^(9-1) = 0.071`

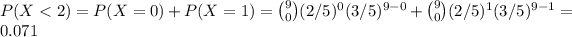
Then, P(X≥ 2) = 1-0.071 = 0.929