Question

A storage shed is to be built in the shape of a box with a square base. It is to have a volume of 686 cubic feet. The concrete for the base costs ​$5 per square​ foot, the material for the roof costs ​$9 per square​ foot, and the material for the sides costs ​$3.50 per square foot. Find the dimensions of the most economical shed.

Answer 1

Therefore the dimension of box is 7 ft by 7 ft by 14 ft.

Explanation:

Given that, a storage shade is be built in the shape of a box with a square base.

Let the height of the box be h and the length of one side of the square base be x.

The area of the square base is = side²

=x²

The volume of the box is = area of the base × height

=x²h

According to the problem,

x²h=686

`\Rightarrow h=(686)/(x^2)` .......(1)

The concrete for the base costs $5 per square foot.

The material for the base costs =$ 5x²

The material for the roof costs $9 per square foot.

The material cost for roof is =$9x²

The material for the sides costs $3.50 per square foot.

The material cost for sides =$(3.50× 4xh )

=$14xh

Total cost =$(5x²+9x²+14xh)

=$(14x²+14 xh)

Let

C = 14x²+14 xh

Putting
`h=(686)/(x^2)`

`C=14x^2+14 x.(686)/(x^2)`

`\Rightarrow C=14x^2+(9604)/(x)`

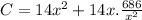
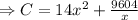
Differentiating with respect to x

`C'= 28x-(9604)/(x^2)`

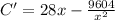
Again differentiating with respect to x

`C''= 28+(19208)/(x^2)`

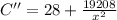
To find the dimension set C'=0

`28x-(9604)/(x^2)=0`

`\Rightarrow 28x=(9604)/(x^2)`

`\Rightarrow x^3=(9604)/(28)`

`\Rightarrow x=7`

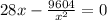
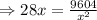
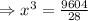
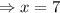
Now,

`C''|_(x=7)= 28+(19208)/(7^2)>0`

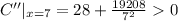
Since at x=7, C''>0, So at x=7 , The cost of material will be minimum.

The height of the box is
`h=(686)/(x^2)`

`=(686)/(7^2)`

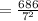
=14 foot

Therefore the dimension of box is 7 ft by 7 ft by 14 ft.

The cost of the material is
`=14x^2+(9604)/(x)`

`=14(7)^2+(9604)/(7)`

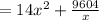
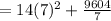
=$2,058