Question

A person hears a pure tone in the 500 to 1000-HzHz range coming from two sources. The sound is loudest at points equidistant from the two sources. To determine exactly what the frequency is, the person moves about and finds that the sound level is minimal at a point 0.24 mm farther from one source than the other.

Answer 1

the frequency of sound is 715Hz

Step-by-step explanation:

The expression for frequency is

f = v / λ

Here, f is the fundamental frequency , v is the speed , λ is the wavelength.

Since the wavelength is twice that of length of half way,

then λ = 2l

substitute the 2l for λvalue in f = v/ λ

f = v / 2l

substitute 343 for v, and 0.24 for l

`f = (343)/(2* 0.24) \\\\f=343/ 0.48\\\\f=714.58Hz`

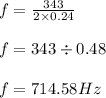
≅715Hz

The expression for frequency is

f = v / λ

If the wavelength is 2l / 3 , the expression for frequency is

`f = (v)/(2l/3)`

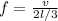
substitute 0,24 for l and 343m/s for v

`f = (343)/(2\ (0.24)/3) \\\\f = (343)/(0.16) \\\\f=2143.5Hz`

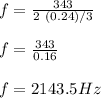
≅2144Hz

Since , the range of the sound heard by the person is 500Hz to 1000Hz .when the wavelength is equal to 2l / 3 the frequency is 2144Hz which is out of range.

Therefore, the frequency of sound is 715Hz