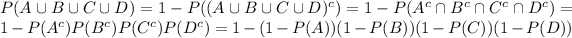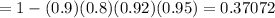Question

A component is assembled in a four-step process. The probability of making a defect in step 1 is 10%; in step 2, 20%; in step 3, 8%; and in step 4, 5%. What is the probability that the component will be defective?

Answer 1

Correct answer is 37.1 % . Explanation is given below :

Production

steps deffective without defects (100) (100-100=0)

1 10 90 100*90/100=90 100-90=10

2 20 80 90*80/100=72 100-72=28

3 8 92 72*92/100=66.24 100-66.24-33.76

4 5 95 66.24*95/100=62.928 100-62.928=37.1

Answer 2

0.37072

Explanation:

Let A be the event that step 1 is defective (P(A) = 10%), B the event that step 2 is defective(P(B) = 20%), C the event that step 3 is defective (P(C) = 8%), D the event that step 4 is defective(P(D) = 5%). Let us suppose that the occurance of a failure at any step is indepent of the other steps.

Recall the following properties

`P(A) = 1- P(A^c)`

`(A\cup B )^c = A^c \cap B^c)`

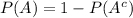
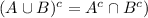
And given A, B, C, D independent , then

`P(A\cap B \cap C \cap D) = P(A)P(B)P(C)P(D)`

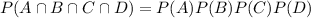
REcall that if the a set of events A,B,C,D are independent, their complements are also indepent.

Since we are asked for the probability of a defective item, this means that at least one of the steps is defective. Then, we are asked for the following probability:

`P(A\cup B \cup C \cup D) = 1 - P((A\cup B \cup C \cup D)^c) = 1 - P(A^c \cap B^c \cap C^c \cap D^c ) = 1 - P(A^c)P(B^c) P(C^c) P(D^c) = 1-(1-P(A))(1-P(B))(1-P(C))(1-P(D))`

`= 1-(0.9)(0.8)(0.92)(0.95) = 0.37072`