Question

The number of minutes needed to drain a bathtub, m, varies inversely as the rate of draining, r. At 20 liters per minute, a bathtub can drain in 8 minutes. How many minutes would it take to drain the bathtub if the rate of drainage was 32 liters per minute?

Answer 1

5 minutes.

Explanation:

We have been given that the number of minutes needed to drain a bathtub, m, varies inversely as the rate of draining, r.

We know that two inversely proportional quantities are in form
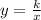`y=(k)/(x)`, where y is inversely proportional with x and k is constant of proportionality.

Upon substituting our given variables in inversely proportion, we will get:

`m=(k)/(r)`

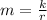
Let us find constant of proportionality using our given information.

`8=(k)/(20)`

`8\cdot 20=(k)/(20)\cdot 20`

`k=160`

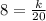
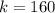
So our required equation would be
`m=(160)/(r)`.

Now, we will substitute
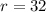`r=32` in our equation to solve for time.

`m=(160)/(32)`

`m=5`

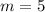
Therefore, it will take 5 minutes to drain the bathtub at a rate of 32 liters per minute.