Question

(6) (Bonus) Determine the Cartesian equation of the surface with spherical coordinate equation rho = 2 cos θ sin φ − 2 sin θ sin φ + 2 cos φ. It turns out this describes a sphere. What is the center and radius of this sphere?

Answer 1

Hence, the sphere has a radius of
`√(3)` and is centered at the point (1,-1,1)

Explanation:

We have the equation

`\rho=2cos\theta cos\phi-2sin\theta sin\phi+2cos\phi`

We have to take into account the relation between coordinates

`\rho=√(x^2+y^2+z^2)\\x=\rho cos\theta sin\phi\\y=\rho sin\theta sin\phi\\z= \rho cos\phi`

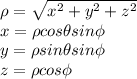
by substituting we have:

`\rho=2[(x)/(\rho)-(y)/(\rho)+(z)/(\rho)]\\\\\rho^2=2x-2y+2z\\\\x^2+y^2+z^2=2x-2y+2z`

We have to complete squares:

`(x^2-2x+1)+(y^2+2y+1)+(z^2-2z+1)-1-1-1=0\\\\(x-1)^2+(y+1)^2+(z-1)^2=3`

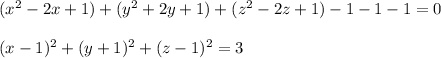
Hence, the sphere has a radius of
`√(3)` and is centered at the point (1,-1,1)

hope this helps!!