Question

Question 1 options: A random sample of 15 drivers from Montana and finds that they drive an average of 12,895 miles annually with a standard deviation of 3801 miles. Find the 96% confidence interval for the population mean of miles driven. You may assume that the number of miles driven per year is normally distributed. Enter the lower and upper bounds for the interval in the following boxes, respectively. Round your answers to the nearest whole number.

Answer 1

Answer: For 96% confidence interval for the population mean of miles driven :

Lower bound = 10,841 miles

Upper bound= 14,949 miles

Explanation:

Here, population standard deviation is unknown and sample size is small , So the formula is used to find the confidence interval for
`\mu` is given by :-

`\overline{x}\pm t^*(s)/(√(n))`

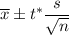
, where n = sample size , = sample mean , t*= two tailed critical value s= sample standard deviation, .

Given,
`\overline{x}` =12,895 miles , s=3,801 miles, n=15 , degree of freedom = 14 [∵df=n-1]

For 96% confidence level ,
`\alpha=0.04`

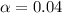
By t-distribution table ,

t-value(two tailed) for
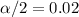`\alpha/2=0.02` and df =14 is t*=2.2638

Now , the 96% confidence interval for the population mean of miles driven will be :

`12895\pm (2.2638)(3801 )/(√(15))\\\\=12895\pm (2.0930)(981.413)\approx12895\pm 2054=(12895- 2054,\ 12895+2054)\\\\=(10,841,\ 14,949)`

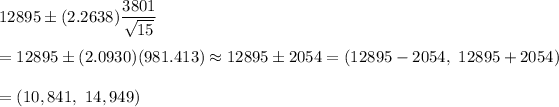
Hence, For 96% confidence interval for the population mean of miles driven :

lower bound = 10,841 miles

upper bound= 14,949 miles