Question

Two flat conductors are placed with their inner faces separated by 15 mm. If the surface charge density on inner face A is 48 pC/m2 and on inner face B is −48 pC/m 2 , calculate the electric potential difference ∆V = VA − VB. Use ǫ0 = 8.85419 × 10−12 C 2 /Nm2 . Answer in units of V.

(part 1 of 2) A proton is accelerated from rest through a potential difference of 25648 V. What is the kinetic energy of this proton after this acceleration? The mass of a proton is 1.673 × 10−27 kg and the elemental charge is 1.602 × 10−19 C. Answer in units of J.

(part 2 of 2) What is the speed of the proton after this acceleration? Answer in units of m/s.

Answer 1

A) potential difference = 10.842V

B) K.E = 4.109x10^-15 J

C) velocity = 2216333.434m/s

Step-by-step explanation:

Detailed explanation and calculation is shown in the image below

Answer 2

part 1 - 4.1*10^{-15}J

part 2 - 2.21*10^6 m/s

Step-by-step explanation:

In this case you have to use the expression

`V=Ed`

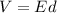
with d the distance between plates. E is given by

`E=(\sigma)/(\epsilon_0)`

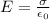
where sigma is the surface charge density and e0 is the dielectric permitivity of vacuum

By replacing we have

`\Delta V=(\sigma d)/(\epsilon_0)=((48*10^(-12)(C)/(m^2))(15*10^(-3)m))/(8.85419*10^(-12)(C^2)/(Nm^2))=8.13*10^(-3)V`

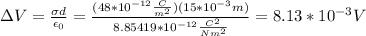
part 1

The kinetic energy is given by

`E_k=q_pV`

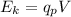
where V is the potential and qp is the charge of the proton. By replacing you have

`E_K=(1.602*10^(-19)C)(25648(J)/(C))=4.1*10^(-15)J`

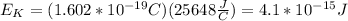
part 2

the speed can be calculated by using

`E_k=(1)/(2)m_pv^2\\\\v=\sqrt{(2E_k)/(m_p)}=\sqrt{(2(4.1*10^(-15)J))/(1.67*10^(-27)kg)}\approx 2.21*10^6(m)/(s)`

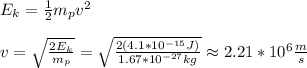
HOPE THIS HELPS!!