Question

128,32,8 what is the next term of the geometric sequence

Answer 1

Given:

The given geometric sequence is 128, 32, 8

We need to determine the next term of the geometric sequence.

Common ratio:

Since, it is given that the sequence is a geometric sequence, then the common ratio is given by

`r=(32)/(128)`

`r=(1)/(4)`

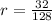
Thus, the common ratio is
`r=(1)/(4)`

Next term:

The next term of the sequence can be determined by multiplying the previous term with the common ratio.

Thus, we have;

Next term =
`8* ((1)/(4))`

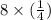
= 2

Thus, the next term is 2.

Hence, the next term of the geometric sequence is 2.