Question

. The U.S. Postal Service will accept a box for domestic shipment only if the sum of its length and girth (distance around) does not exceed 108 inches. What dimensions will give a box with a square end the largest volume

Answer 1

Dimension a = 18 , b= 36 will give a box with a square end the largest volume

Explanation:

Given -

sum of box length and girth (distance around) does not exceed 108 inches.

Let b be the lenth of box and a be the side of square

b + 4a = 108

b = 108 - 4a

Volume of box =
`area * lenth`

=
`a^2* b`

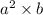
V =
`a^2* b`

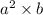
puting the value of b

V =
`a^2 ( 108 - 4a )`

`V = 108a^2 - 4a^3`

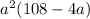
To find the maximum value of V

(1) we differentiate it

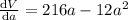
`\frac{\mathrm{d} V}{\mathrm{d} a} = 216a - 12a^2`

(2)
`\frac{\mathrm{d} V}{\mathrm{d} a} = 0`

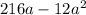`216a - 12a^2` = 0

12a ( 18 - a ) =

a = 0 and a = 18

(3) putting the value of a if
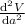`\frac{\mathrm{d^2} V}{\mathrm{d} a^2}` = negative then the value for a ,V is maximum

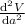`\frac{\mathrm{d^2} V}{\mathrm{d} a^2}` = 216 - 24a

put the value of a = 0 ,
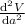`\frac{\mathrm{d^2} V}{\mathrm{d} a^2}` = 216

put the value of a = 18 ,
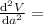`\frac{\mathrm{d^2} V}{\mathrm{d} a^2} =` negative

for the value of a =18 V gives maximum value

Max volume =
`108*18^2 - 4*18^3`

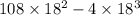
= 11664

a = 18 , b = 108 - 4a =
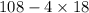`108 - 4* 18` = 36