Answer:
The frictional force
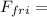 6.446 N
6.446 N
The acceleration of the block a = 6.04
Step-by-step explanation:
Mass of the block = 3.9 kg
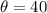 °
°
 = 0.22
= 0.22
(a). The frictional force is given by
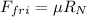

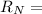 3.9 × 9.81 ×
3.9 × 9.81 ×
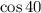
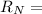 29.3 N
29.3 N
Therefore the frictional force
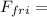 0.22 × 29.3
0.22 × 29.3
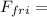 6.446 N
6.446 N
(b). Block acceleration is given by
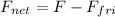
F = 30 N
 = 6.446 N
= 6.446 N
 = 30 - 6.446
= 30 - 6.446
 = 23.554 N
= 23.554 N
The net force acting on the block is given by
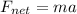
23.554 = 3.9 × a
a = 6.04
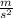
This is the acceleration of the block.