Question

A solid sphere, a solid cylinder, and a hoop all have the same mass and radius. Each are sent down identical inclined planes starting from rest. Their kinetic energies at the bottom of the incline are Ksphere, Kcylinder, and Khoop. Which of the following is true? (Hint: you should not need to calculate their different velocities at the bottom of the incline to answer this).a.Ksphere > Kcylinder

b.Khoop > Kspherec.Khoop > Kcylinder
d.Kcylinder > Khoop
e.No answer above is correct

Answer 1

Step-by-step explanation:

The velocity of that object at the bottom will be highest whose acceleration will be highest .

acceleration of a body rolling down an inclined plane

a = g sinθ / (1 +
`(k^2)/(r^2)` )

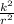k is radius of gyration , r is radius of the object , θ is inclination of plane .

for sphere moment of inertia M = 2 / 5 m r²

radius of gyration k

k² = 2/5 r²

k² / r² = 2 / 5

= 0.4

for cylinder

moment of inertia M = 1 / 2 m r²

radius of gyration k

k² = 1 /2 r²

k² / r² = 1/2

= 0.5

For hoop

moment of inertia M = m r²

radius of gyration k

k² = r²

k² / r² = 1

=

So the value of k² / r² is maximum for hoop and minimum for sphere .

hence acceleration will be minimum for hoop and maximum for sphere

so Ksphere > Kcylinder> Khoop .