Question

You are driving along a highway at 35.0 m/s when you hear the siren of a police car approaching you from behind and you perceive the frequency as 1370 Hz. You are relieved that he is in pursuit of a different speeder when he continues past you, but now you perceive the frequency as 1330 Hz. The speed of sound in air is (a)What is the speed of the police car? [3] (b) What is the original frequency of siren from the police car?[2] (c) At what speed you need to drive if you want to hear the same frequency as the originally emitted police siren coming from behind?[1]

Answer 1

Step-by-step explanation:

In the first case you can use the expression for the Doppler effect when the source is getting closer and getting away

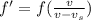`f'=f((v)/(v-v_(s)))` ( 1 )

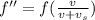`f''=f((v)/(v+v_s))` ( 2 )

f' = perceived frequency when the source is getting closer

f'' = perceived frequency when the source is getting away

f = source frequency

v = relative speed

vs = sound speed

by dividing (1) and (2) you have

`(f')/(f'')=(f)/(f)((v)/(v-v_s))/((v)/(v+v_s))=(v+v_s)/(v-v_s)\\\\f'v-f'v_s=f''v+f''v_s\\\\v(f'-f'')=v_s(f''+f')\\\\v=v_s(f''+f')/(f'-f'')=(340(m)/(s))(1370Hz+1330Hz)/(1370Hz-1330Hz)=67.5(m)/(s)`

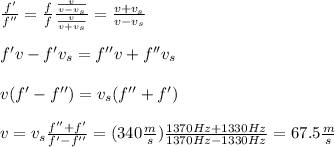
but this is the relative velocity, you have that

`v=v_(sir)-v_(car)\\v_(sir)=v+v_(car)=67.5(m)/(s)+35(m)/(s)=102.5(m)/(s)`

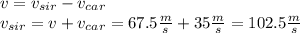
a. hence, the speed of the police car is 102.5m/s