Answer:
The equation of an ellipse is
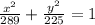 and the vertical width of ellipse at x = 6 inch from centre of ellipse is 28.06 inch.
and the vertical width of ellipse at x = 6 inch from centre of ellipse is 28.06 inch.
Explanation:
We know that, the equation of an ellipse with horizontal major axis with centre at (0,0):
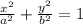 ------------------------------------(1)
------------------------------------(1)
According to the question,
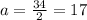 inch⇒
inch⇒
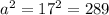
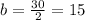 inch⇒
inch⇒
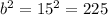
After putting the value of
 and
and
 in the equation(1), we get
in the equation(1), we get
The equation of an ellipse is
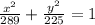
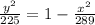
⇒
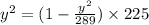
⇒
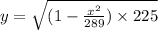 -----------------------------(2)
-----------------------------(2)
At
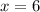 inch from centre(0,0) of ellipse,
inch from centre(0,0) of ellipse,
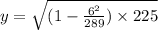
⇒
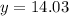 inch
inch
Therefore, the total vertical width of ellipse at x = 6 inch from centre of ellipse =
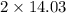 = 28.06 inch
= 28.06 inch