Answer:
Required (a) vertical tangent at (1,0) (b) horizontal tangent at (-1,2) (c) concave upward ob (1,0) (d) concave downward on (-1,2).
Explanation:
Consider a parametric curve,
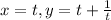
Then substitute value of x in y we get,
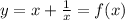
(a) To find points where vertical or horizintal tangent are meet we have to take,
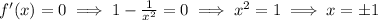
when,
x=1, y=0
x=-1, y=2
Now at point (1,0),
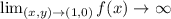
So at this point there is a vertical tangent.
(b) And (-1,2) is then the point where horizontal tangent meet.
To find point of interval where function is concave upward or downward we have to derivative f(x) with respect to x twice that is,
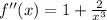
(c) At x=1, f''(1)=3>0, that means on the interval (1,0) the function is concave upward.
(d) At x=-1, f''(-1)=-1, which imply on the interval (-1,2) the funcrion is concave downward.