Question

Consider the parametric curve a. Find points on the parametric curve where the tangent lines are vertical. b. Find points on the parametric curve where the tangent lines are horizontal. c. Find the interval(s), in terms of , where the parametric curve is concave upward. d. Find the interval(s), in terms of , where the parametric curve is concave downward

Answer 1

Required (a) vertical tangent at (1,0) (b) horizontal tangent at (-1,2) (c) concave upward ob (1,0) (d) concave downward on (-1,2).

Explanation:

Consider a parametric curve,

`x=t, y=t+(1)/(t)`

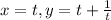
Then substitute value of x in y we get,

`y=x+(1)/(x)=f(x)`

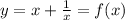
(a) To find points where vertical or horizintal tangent are meet we have to take,

`f'(x)=0\implies 1-(1)/(x^2)=0\implies x^2=1\implies x=\pm 1`

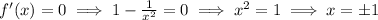
when,

x=1, y=0

x=-1, y=2

Now at point (1,0),

`\lim_((x,y)\to (1,0))f(x)\to \infty`

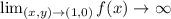
So at this point there is a vertical tangent.

(b) And (-1,2) is then the point where horizontal tangent meet.

To find point of interval where function is concave upward or downward we have to derivative f(x) with respect to x twice that is,

`f''(x)=1+ (2)/(x^3)`

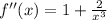
(c) At x=1, f''(1)=3>0, that means on the interval (1,0) the function is concave upward.

(d) At x=-1, f''(-1)=-1, which imply on the interval (-1,2) the funcrion is concave downward.