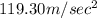Question

A wheel with a tire mounted on it rotates at the constant rate of 2.97 revolutions per second. Find the radial acceleration of a tack stuck in the tire at a distance of 32.7 cm from the rotation axis.

Answer 1

Angular acceleration will be equal to
`119.30m/sec^2`

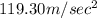
Step-by-step explanation:

We have given that wheel tires are moving with constant rate of
`\omega =2.97rev/sec=2.97* 2\pi =19.10rad/sec`

Distance is given r = 32.7 cm = 0.327 m

Linear velocity is given by
`v=\omega r=19.01* 0.327=6.24m/sec`

Wee to have to find the angular acceleration

Angular acceleration is equal to
`a=(v^2)/(r)=(6.24^2)/(0.327)=119.30m/sec^2`

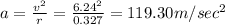
So angular acceleration will be equal to
`119.30m/sec^2`