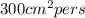Question

The length of a rectangle is increasing at a rate of 8cm/s8cm/s and its width is increasing at a rate of 5cm/s5cm/s. When the length is 20cm20cm and the width is 25cm,25cm, how fast is the area of the rectangle increasing

Answer 1

The area of the given rectangle increasing when l=20cm and w=25 cm by fast is
`300cm^2 per s`

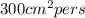
Explanation:

Given that the length of a rectangle is increasing at a rate of 8cm per s and its width is increasing at a rate of 5cm per s.

To find the how fast is the area of the rectangle increasing when the length is 20 cm and the width is 25 cm:

Let l be the Length of Rectangle (cm)

Let w be the Width of Rectangle (cm)

Let A be the Area of Rectangle (
`cm^2`)

Let t be the Time (s)

From the given we can write

cm per s and

cm per s

The formula for Area of the rectangle is:

A=lw square units

Differentiating with respect to t

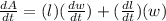`(dA)/(dt)=(l)((dw)/(dt))+((dl)/(dt))(w)` ( by using the product rule formula
`(d(uv))/(dx)=u((dv)/(dx))+(du)/(dx)(v)`)

`=l(5)+8(w)`

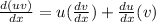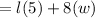
when l=20 and w=25

`=(20)(5)+8(25)`

`=100+200`

`=300`

∴
`(dA)/(dx)=300 cm^2 per s`

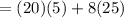
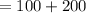
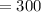
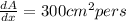
∴ the area of the rectangle increasing by fast is
`300cm^2 per s`