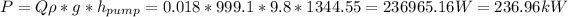Answer:
The required pumping head is 1344.55 m and the pumping power is 236.96 kW
Step-by-step explanation:
The energy equation is equal to:
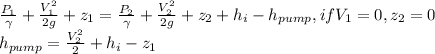
For the pipe 1, the flow velocity is:
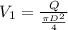
Q = 18 L/s = 0.018 m³/s
D = 6 cm = 0.06 m
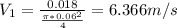
The Reynold´s number is:
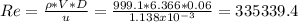
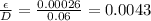
Using the graph of Moody, I will select the f value at 0.0043 and 335339.4, as 0.02941
The head of pipe 1 is:
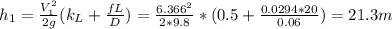
For the pipe 2, the flow velocity is:
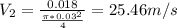
The Reynold´s number is:
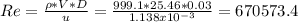
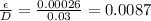
The head of pipe 1 is:
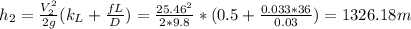
The total head is:
hi = 1326.18 + 21.3 = 1347.48 m
The required pump head is:
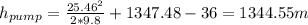
The required pumping power is: