Answer:
(g)

(h)
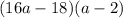
(i)
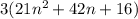
Explanation:
To factor a quadratic in the form

- Find 2 two numbers (
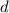 and
and
 ) that multiply to
) that multiply to
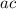 and sum to
and sum to

- Rewrite
 as the sum of these 2 numbers:
as the sum of these 2 numbers:

- Factorize the first two terms and the last two terms separately, then factor out the comment term.
Question (g)
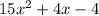
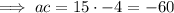
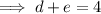
Factors of 60: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60
Therefore, the two numbers (d and e) that multiply to -60 and sum to 4 are:
10 and -6
Rewrite
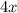 as
as
 :
:
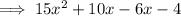
Factories first two terms and last two terms separately:
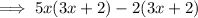
Factor out common term
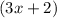 :
:
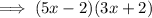
Question (h)
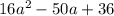


Factors of 576: 1, 2, 3, 4, 6, 8, 9, 12, 16, 18, 24, 32, 36, 48, 64, 72, 96, 144, 192, 288, 576
Therefore, the two numbers that multiply to 576 and sum to -50 are:
-32 and -18
Rewrite
 as
as
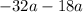 :
:
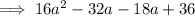
Factories first two terms and last two terms separately:
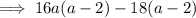
Factor out common term
 :
:
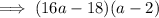
Question (i)

Factor out common term 3:
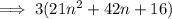
This cannot be factored any further.