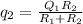Question

This sphere is now connected by a long, thin conducting wire to another sphere of radius R2 that is several meters from the first sphere. Before the connection is made, this second sphere is uncharged. After electrostatic equilibrium has been reached, what is the total charge on each sphere? Assume that the amount of charge on the wire is much less than the charge on each sphere.

Answer 1

Here is the full question

A metal sphere with Radius R₁ has a charge Q₁. Take the electric potential to be zero at an infinite distance from the sphere

a) What are the electric field and electric potential at the surface of the sphere?

This sphere is now connected by a long, thin conducting wire to another sphere of radius R₂ that is several meters from the first sphere. Before the connection is made, this second sphere is uncharged. After electrostatic equilibrium has been reached:

b) what is the total charge on each sphere?

Assume that the amount of charge on the wire is much less than the charge on each sphere.

Answer:

a) The electric field (E) at the surface is the first sphere =
`(1)/(4 \pi \epsilon _0)(Q_1)/(R_1^2)`

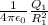
The electric potential (V) at the surface of the first sphere =
`(1)/(4 \pi \epsilon _0)(Q_1)/(R_1)`

=
`ER_1`

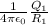
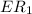
b)

The total charge of the first sphere
`q_1 = (Q_1R_1)/(R_1+R_2)`

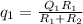
The total charge of the second sphere
`q_2= (Q_1R_2)/(R_1+R_2)`

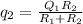
Step-by-step explanation:

Given that;

the radius of the sphere = R

The radius of the first sphere =
`R_1`

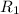
The radius of the second sphere =
`R_2`

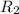
Charge on the first sphere =
`Q_1`

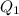
a) The electric field (E) at the surface is the first sphere =
`(1)/(4 \pi \epsilon _0)(Q_1)/(R_1^2)`

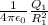
The electric potential (V) at the surface of the first sphere =
`(1)/(4 \pi \epsilon _0)(Q_1)/(R_1)`

=
`ER_1`

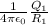
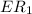
b) From the question. before the part b question; we learnt that the first sphere is now connected to another sphere;

Now that the two sphere are joined . Charges flows from one to another until their potentials are equal.

As Such; We use
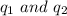`q_1 \ and \ q_2` to represent their charges respectively

The potential on the surface of the first sphere;

`V_1 = (1)/(4 \pi \epsilon _0)(q_1)/(R_1)`

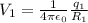
The potential on the surface of the second sphere;

`V_2 = (1)/(4 \pi \epsilon _0)(q_2)/(R_2)`

`V_1=V_2`

∴

`(1)/(4 \pi \epsilon _0)(q_1)/(R_1)= (1)/(4 \pi \epsilon _0)(q_2)/(R_2)`

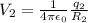
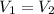
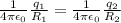
Thus, we can say :

`(q_1)/(q_2)= (R_1)/(R_2)`

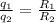
and
`Q_1 = q_1 + q_2`

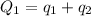
As such ;

The total charge of the first sphere
`q_1 = (Q_1R_1)/(R_1+R_2)`

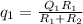
The total charge of the second sphere
`q_2= (Q_1R_2)/(R_1+R_2)`