Answer:
Probability that the sample proportion is between 0.70 and 0.85 is 0.8688.
Explanation:
We are given that in a local university, 80% of the students live in the dormitories.
A random sample of 80 university students is selected to participate in a particular study.
Let
 = sample proportion (the proportion living in the dormitories)
= sample proportion (the proportion living in the dormitories)
The z-score probability distribution for sample proportion is given by;
Z =
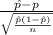 ~ N(0,1)
~ N(0,1)
where,
 = sample proportion
= sample proportion
p = population proportion of the students who live in the dormitories = 57%
n = sample of students = 80
The Z-score measures how many standard deviations the measure is away from the mean. After finding the Z-score, we look at the z-score table and find the p-value (area) associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X.
So, probability that the sample proportion (the proportion living in the dormitories) is between 0.70 and 0.85 is given by = P(0.70 <
 < 0.85)
< 0.85)
P(0.70 <
 < 0.85) = P(
< 0.85) = P(
 < 0.85) - P(
< 0.85) - P(

 0.70)
0.70)
P(
 < 0.85) = P(
< 0.85) = P(
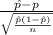 <
<
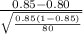 ) = P(Z < 1.25) = 0.89435
) = P(Z < 1.25) = 0.89435
P(

 0.70) = P(
0.70) = P(
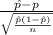

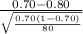 ) = P(Z
) = P(Z
 -1.95) = 1 - P(Z < 1.95)
-1.95) = 1 - P(Z < 1.95)
= 1 - 0.97441 = 0.02559
Now, in the z table the P(Z
 x) or P(Z < x) is given. So, the above probability is calculated by looking at the value of x = 1.25 and x = 1.95 in the z table which has an area of 0.89435 and 0.97441.
x) or P(Z < x) is given. So, the above probability is calculated by looking at the value of x = 1.25 and x = 1.95 in the z table which has an area of 0.89435 and 0.97441.
Therefore, P(0.70 <
 < 0.85) = 0.89435 - 0.02559 = 0.8688
< 0.85) = 0.89435 - 0.02559 = 0.8688
Hence, probability that the sample proportion is between 0.70 and 0.85 is 0.8688.