Answer:
The maximum speed at which the car can safety travel around the track is 18.6m/s.
Step-by-step explanation:
Since the car is in circular motion, there has to be a centripetal force
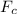 . In this case, the only force that applies for that is the static frictional force
. In this case, the only force that applies for that is the static frictional force
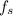 between the tires and the track. Then, we can write that:
between the tires and the track. Then, we can write that:
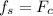
And since
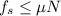 and
and
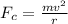 , we have:
, we have:

Now, if we write the vertical equation of motion of the car (in which there are only the weight and the normal force), we obtain:
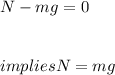
Substituting this expression for
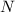 and solving for
and solving for
 , we get:
, we get:
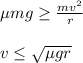
Finally, plugging in the given values for the coefficient of friction and the radius of the track, we have:
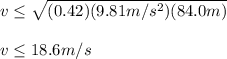
It means that in its maximum value, the speed of the car is equal to 18.6m/s.