Given:
DE = (6x - 9) cm
EF = (4x + 4) cm
LM = 14 cm
MN = 16 cm
To find:
The value of x.
Solution:
If three or more parallel lines intersect two transversals, then they cut off the transversals proportionally.
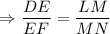
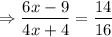
Do cross multiplication.
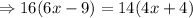
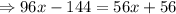
Add 144 on both sides.
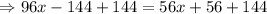
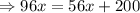
Subtract 56x from both sides.
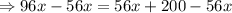
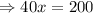
Divide by 40 on both sides, we get
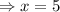
The value of x is 5.