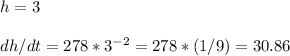Question

An inverted pyramid is being filled with water at a constant rate of 25 cubic centimeters per second. The pyramid, at the top, has the shape of a square with sides of length 3 cm, and the height is 10 cm. Find the rate at which the water level is rising when the water level is 3 cm.

Answer 1

When the water level is 3 cm, the rate at which the water level is rising is 30.86 cm/s.

Explanation:

We first have to relate the height H of the pyramid with the volume V.

The volume of the pyramid is V=Sh/3, being S: area of the base square, and h: height of the pyramid.

The base is changing as the pyramid is filled with water.

Then, the volume for every height is:

`V(t)=[L(t)]^2h(t)/3`

The side of the square will grow linearly with the height. They start at H=0 and L=0 at the bottom of the pyramid, and they end at H=10 and L=3.

So we have:

`L=(3/10)h=0.3h`

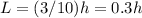
If we replace in the volume equation we have:

`V=L^2h/3=(0.3h)^2h/3=0.09h^3/3=0.03h^3`

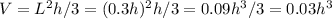
We know that the rate of variation of the volume in time is contant and equal to 25 cm3:

`dV/dt=25`

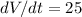
We can derive the volume equation to calculate the variation of h in time:

`dV/dt=3(0.03)h^2*(dh/dt)=0.09h^2*(dh/dt)=25\\\\dh/dt=(25/0.09)h^(-2)=278h^(-2)`

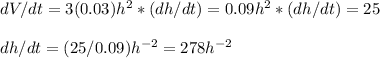
The rate of variation of the height in time is dh/dt=278h^(-2). The units are cm/s.

When the water level is 3 cm, the rate at which the water level is rising is:

`h=3\\\\dh/dt=278*3^(-2)=278*(1/9)=30.86`