Answer:
Combined velocity is 402.35 m/s.
Step-by-step explanation:
Given that,
Mass of the bullet, m = 0.045 kg
Initial speed of the bullet, v = 456 m/s
Mass of the sponge, m' = 0.006 kg
Initial speed of the sponge is 0 as it was at rest. The momentum remains conserved in this case. The bullet is embedded in the sponge, it is a case of inelastic collision. So,
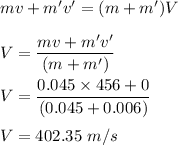
So, the combined bullet and sponge velocity after the perfectly inelastic collision is 402.35 m/s.