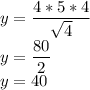Question

y varies jointly as a and b and inversely as the square root of c. y equals 16y=16 when a equals 4 comma=4, b equals 5 commab=5, and c equals 25.c=25. Find y when a equals 5 comma=5, b equals 4 commab=4, and c equals 4.c=4. Find y when a equals 5 commaa=5, b equals 4 commab=4, and c equals 4.c=4.

Answer 1

y=40

Explanation:

If y varies jointly as a and b

y∝ab

If y varies inversely as the square root of c

y∝
`(1)/(√(c) )`

Combining the two

y∝
`(ab)/(√(c) )`

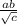
Introducing Variation Constant

`y=(kab)/(√(c) )`

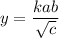
y=16, When a=4, b=5, c=25

`16=(k*4*5)/(√(25) )\\16=(20k)/(5)\\20k=16*5\\20k=80\\k=4`

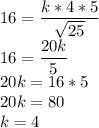
Therefore the equation connecting a. b and c is:

`y=(4ab)/(√(c) )`

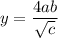
We are to determine y when a=5, b=4 and c=4

`y=(4*5*4)/(√(4) )\\y=(80)/(2 )\\y=40`

Answer 2

Y = 40

Explanation:

When y varies jointly as a and b and inversely as the square root of c,we have an equation that looks like this

Y = kab/√c

Where k is the constant needed to get the proper values.

When Y is 6

A = 4,b = 5, and c = 25

16= (4 × 5 × k)/√25

16 = 20k/√25

Now cross multiply to get

16 × √25 = 20k

16 × 5 = 20k

80 = 20k

K = 4

So we now need to find Y when a is 5,b = 4 and = 4

Remember that k = 4

Y = kab/√c

Y = 4 × 5 × 4 ÷ √4

Y = 80÷2

Y = 40