Answer:
Option C
Explanation:
We have to minimize the standard error of the proportion.
We have a finite population (one for the customers who shop at one store location and other bigger that is for the customers who shop at the stores citywide).
The standard error for a finite population can be written as:
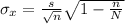
For each population, the higher the sample size, the less variablity will have in the estimation of the proportion. So, we are left with option C and D.
We can calculate the standard error for each posibility and compare:
c) Sample n=200 customers from the roughly N=2000 customers who shop at one store location.
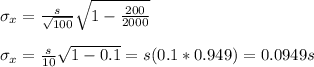
d) Sample 300 customers from the roughly 20,000 customers who shop at the stores citywide.
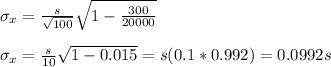
It will give less variability the Option C.
It is assumed that sampling only one store is representative of the parameter of the population of study.