Question

Shameel has a flight to catch on Monday morning. His father will give him a ride to the airport. If it rains, the traffic will be bad and the probability that he will miss his flight is 0.04. If it doesn't rain, the probability that he will miss his flight is 0.03. The probability that it will rain on Monday is 0.26. Are rain and Shameel missing his flight independent events

Answer 1

The events rain and Shameel missing his flight are not independent events.

Explanation:

Independent events are those events that are not affected by the occurrence (or no occurrence) of other events. These events do not affect the probability of another even taking place.

For example, the events of winning a lottery and being late for work are independent.

If events A and B are independent then:

`P(A\cap B)=P(A)* P(B)`

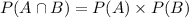
And the conditional probability of B given A is:

`P(B|A)=P(B)`

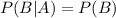
Denote the events as follows:

X = Shameel misses his flight

Y = it rains on Monday morning.

The information provided are:

`P(X|Y)=0.04\\P(X|Y^(c))=0.03\\P(Y)=0.26`

The law of total probability states that:

`P(B)=P(B|A)P(A)+P(B|A^(c))P(A^(c))`

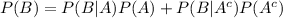
Use this law to compute the probability of X as follows:

`P(X)=P(X|Y)P(Y)+P(X|Y^(c))P(Y^(c))\\=(0.04* 0.26)+(0.03* (1-0.26))\\=0.0104+0.0222\\=0.0326\\\approx0.033`

If the events X and Y are independent then,

`P(X|Y)=P(X)`

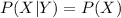
But the value of P (X) is 0.033.

That is,
`P(X|Y)\\eq P(X)`.

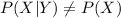Thus, the events rain and Shameel missing his flight are not independent events.