Question

The average number of customers arriving at an ATM machine is 27 per hour during lunch hours. Use equation to denote the number of arrivals in a 5 minute time interval. Assume the customers arrive independently and the number of arrivals within each 5 minutes follows a Poisson distribution. Keep at least 4 decimal digits if the result has more decimal digits. The probability that exactly 2 customers arrive in a given 5 minute interval is closest to

Answer 1

The probability that exactly 2 customers arrive in a given 5 minute interval = 0.2667

Explanation:

Given -

The average number of customers arriving at an ATM machine is 27 per hour during lunch hours. then the average number of customers arriving at an ATM machine n a 5 minute time interval =
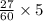`(27)/(60) * 5` = 2.25

average number of customers arriving at an ATM machine n a 5 minute time interval
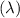`(\lambda )` = 2.25

Let X denote the no of customer arrivals in a 5 minute time interval

The probability that exactly 2 customers arrive in a given 5 minute interval =

P( X = 2 ) =
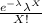`(e^(-\lambda )\lambda ^(X))/(X!)` ( Using poision distribution )

=
`(e^(-2.25) (2.25)^2)/(2!)`

=
`(.1054 * 5.0625)/(2)`

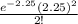
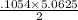
= 0.2667