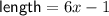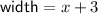Question

Could someone please help me really quickly?

Answer 1

`6x^2 +17x -3\\\\=6x^2 +18x-x-3\\ \\=6x(x+3)-(x+3)\\ \\=(x+3)(6x-1)\\\\\text{The length and width of the rectangle are}~ (6x-1)~ \text{and}~ (x+3)`

Answer 2

`\textsf{length}=6x - 1`

`\textsf{width}=x+3`

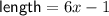
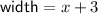
Explanation:

Area of a rectangle = length × width

Given area:
`A=6x^2+17x-3`

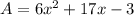
Therefore,
`6x^2+17x-3=\sf length \cdot width`

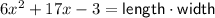
To find the length and width, we need to factorize the given expression for area.

To factor a quadratic in the form
`ax^2+bx+c`

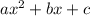
• Find 2 two numbers (d and e) that multiply to ac and sum to b
• Rewrite b as the sum of these 2 numbers: d + e = b
• Factorize the first two terms and the last two terms separately, then factor out the comment term.

`6x^2+17x-3 \implies a=6, b=17, c=-3`

`ac=6 \cdot -3=-18`

`d+e=17`

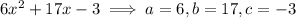
So we are looking for a pair of numbers that multiply to -18 and sum to 17.

Factors of 18: 1, 2, 3, 6, 9, 18

Therefore, the two numbers (d and e) that multiply to -18 and sum to 17 are:

18 and -1

Rewrite
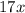`17x` as
`+18x-x`:

`\implies 6x^2+18x-x-3`

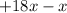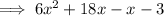
Factor first two terms and last two terms separately:

`\implies 6x(x+3)-1(x+3)`

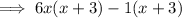
Factor out common term
`(x+3)`:

`\implies (6x-1)(x+3)`

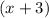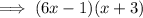
As length > width,

`\textsf{length}=6x - 1`

`\textsf{width}=x+3`