Question

Water at atmospheric pressure boils on the surface of a large horizontal copper tube. The heat flux is 90% of the critical value. The tube surface is initially scored; however, over time the effects of scoring diminish and the boiling eventually exhibits behavior similar to that associated with a polished surface. Determine the tube surface temperature immediately after installation and after prolonged service. Assume nucleate boiling at outer surface of tube.

Answer 1

The tube surface temperature immediately after installation is 120.4°C and after prolonged service is 110.8°C

Step-by-step explanation:

The properties of water at 100°C and 1 atm are:

pL = 957.9 kg/m³

pV = 0.596 kg/m³

ΔHL = 2257 kJ/kg

CpL = 4.217 kJ/kg K

uL = 279x10⁻⁶Ns/m²

KL = 0.68 W/m K

σ = 58.9x10³N/m

When the water boils on the surface its heat flux is:

`q=0.149h_(fg) \rho _(v) ((\sigma (\rho _(L)-\rho _(v)))/(\rho _(v)^(2) ) )^(1/4) =0.149*2257*0.596*((58.9x10^(-3)*(957.9-0.596) )/(0.596^(2) ) )^(1/4) =18703.42W/m^(2)`

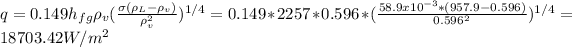
For copper-water, the properties are:

Cfg = 0.0128

The heat flux is:

qn = 0.9 * 18703.42 = 16833.078 W/m²

`q_(n) =uK((g(\rho_(L)-\rho _(v)) )/(\sigma ))^(1/2) ((c_(pL)*deltaT )/(c_(fg)h_(fg)Pr ) \\16833.078=279x10^(-6) *2257x10^(3) ((9.8*(957.9-0.596))/(0.596) )^(1/2) *((4.127x10^(3)*delta-T )/(0.0128*2257x10^(3)*1.76 ) )^(3) \\delta-T=20.4`

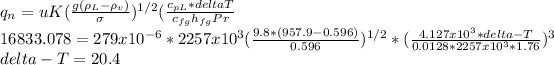
The tube surface temperature immediately after installation is:

Tinst = 100 + 20.4 = 120.4°C

For rough surfaces, Cfg = 0.0068. Using the same equation:

ΔT = 10.8°C

The tube surface temperature after prolonged service is:

Tprolo = 100 + 10.8 = 110.8°C