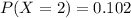Question

The following represents the probability distribution of the number of classes a student takes in a spring semester.

x P(x) 1 0.115 2 3 0.422 4 0.312 5 0.034 6 0.015

Find the missing probability.

Answer 1

X 1 2 3 4 5 6

P(X) 0.115 a 0.422 0.312 0.034 0.015

If we want a probability distribution we need to satisfy two important conditions:

1)
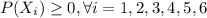
`P(X_i) \geq 0, \forall i=1,2,3,4,5,6`

2)
`\sum_(i=1)^n P(X_i) =1`

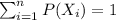
And using the second condition we have this:

`0.115+a+0.422+0.312 +0.034 +0.015=1`

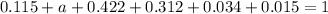
With a the probability associated with the value of X=2 and solving for a we got:

`a = 1-0.115-0.422-0.312-0.034-0.015= 0.102`

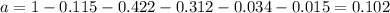
So then for this case
`P(X=2) = 0.102`

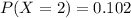
Explanation:

Let X the random variable that represent the number of classes that a student takes

For this case we have the following probability distribution given:

X 1 2 3 4 5 6

P(X) 0.115 a 0.422 0.312 0.034 0.015

If we want a probability distribution we need to satisfy two important conditions:

1)
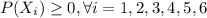
`P(X_i) \geq 0, \forall i=1,2,3,4,5,6`

2)
`\sum_(i=1)^n P(X_i) =1`

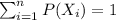
And using the second condition we have this:

`0.115+a+0.422+0.312 +0.034 +0.015=1`

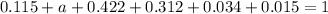
With a the probability associated with the value of X=2 and solving for a we got:

`a = 1-0.115-0.422-0.312-0.034-0.015= 0.102`

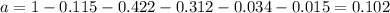
So then for this case
`P(X=2) = 0.102`