Question

The birth rate in an area is increasing by 6% per annum. If there are 20,000 children born in this area in 2009.

a. How many children will be born in 2018 in this area?
b. How many children in total will be born in this area between the years 2009 to 2018 inclusive?

Answer 1

a) Rounding to the nearest whole number, the number of children born in 2018 would be 33,790.

b) Rounding to the nearest whole number, 263,616 children will be born in the area between the years 2009 to 2018 inclusive.

Explanation:

Growth rate of children = 6% per annum

Number of children born in 2009 = A = 20,000

Part a) Number of children born in 2018.

Since the number of children being born is growing by 6% each year, the growth of children being born can be modeled by an exponential growth model shown by the equation below:

`A_(t)=A(1+r)^t`

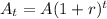
This model shows that the initial number/population was A, and it grew by r% each year.
`A_(t)` is the number/population after t years.

For our case, initial population is equal to A = 20,000

r = growth rate = 6% = 0.06

For 2018 the number of years since 2009 will be 9. So t = 9

Using these values in the formula, we get:

`A_(9)=20000(1+0.06)^(9)\\\\ A_(9)=33790`

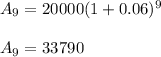
Thus, rounding to the nearest whole number, the number of children born in 2018 would be 33,790.

Part b) Number of children born from 2009 to 2018.

Number of children born in 2009 = 20,000

Since the number of children is growing by 6% per year, this means the number of children in a year will be 1.06 times the number of children born in previous year. Therefore,

Number of children born in 2010 =20000 x (1.06)

Number of children born in 2011 = 20,000 x (1.06)²

If you observe these terms:

20000, 20000 x (1.06), 20,000 x (1.06)² ...

You will notice that these terms for a Geometric Progression as the ratio of 2 consecutive terms is the same i.e. 1.06

The first term of the G.P is A = 20,000

The common ratio is r = 1.06

Finding number of children being born from 2009 to 2018 means finding the sum of first 10 terms of the sequence. The formula to calculate the sum of a G.P is:

`S_(n)=(A(1-r^(n)))/(1-r)`

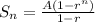
Here n represents the number of terms for which we need to find the sum. So n = 10.

Substituting the values in this formula, we get:

`S_(10)=(20000(1-1.06^(10)))/(1-1.06)=263,616`

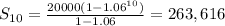
Thus, rounding to the nearest whole number, 263,616 children will be born in the area between the years 2009 to 2018 inclusive.

Note: For part a, the variable t represents the number of years after 2009. That's why 2018 was year 9. For part b, 2009 is considered as first term of the G.P, and this makes 2018 the 10th term.