Question

At a given temperature and pressure, a sample of Gas A is observed to diffuse twice as fast as a sample of a different gas, B. Based on this: a.The molar mass of A is one fourth that of B b.The molar mass of A is one half that of B c.The molar mass of A is four times that of B d.The molar mass of A is 1.414 times that of B e.The molar mass of A is 0.707 times that of B

Answer 1

Answer: The molar mass of A is one fourth that of B

Step-by-step explanation:

To calculate the rate of diffusion of gas, we use Graham's Law.

This law states that the rate of diffusion of gas is inversely proportional to the square root of the molar mass of the gas. The equation given by this law follows the equation:

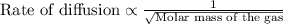
`\text{Rate of diffusion}\propto \frac{1}{\sqrt{\text{Molar mass of the gas}}}`

So,

`\frac{\text{Rate}_A}{\text{Rate}_(B)}=\sqrt{(M_(B))/(M_(A))}`

We are given:

Rate of diffusion of A =
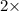`2*` Rate of diffusion of B

Putting values in above equation, we get:

`2=\sqrt{(M_(B))/(M_(A))}`

`4={(M_(B))/(M_(A))}`

`M_(A)={(M_(B))/(4)`

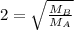
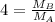
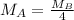
Thus the molar mass of A is one fourth that of B