Question

What is the measure of each angle

Answer 1

Given:

Let x and y denote the supplementary angles.

Given that an angle measures 102.8° more than the measure of its supplementary angles.

This can be written in expression as,

`y=102.8^(\circ)+x`

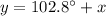
Measure of two angles:

Since, the two angles are supplementary and the supplementary angles add up to 180°

Thus, we have;

`x+y=180^(\circ)`

Substituting
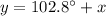`y=102.8^(\circ)+x` in the above formula, we get;

`x+102.8^(\circ)+x=180^(\circ)`

`2x+102.8^(\circ)=180^(\circ)`

`2x=77.2^(\circ)`

`x=38.6^(\circ)`

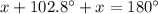
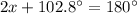
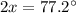
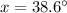
Thus, the measure of one angle is 38.6°

Substituting
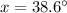`x=38.6^(\circ)` in the equation
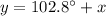`y=102.8^(\circ)+x`, we get;

`y=102.8^(\circ)+38.6^(\circ)`

`y=141.4^(\circ)`

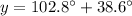
Thus, the measure of the other angle is 141.4°

Hence, the measure of the two angles are 38.6° and 141.4°