Complete Question
If a power utility were able to replace an existing 500 kV transmission line with one operating at 1 MV, it would change the amount of heat produced in the transmission line to
a four times the previous value.
b two times the previous value.
c one-fourth of the previous value.
d The amount of heat produced would remain the same.
e one-half of the previous value.
f none of these.
Answer:
Option C is the correct answer
Step-by-step explanation:
When the voltage is 500kV
The power is
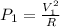
When the voltage is 1MV = 2 × 500kV
The power is
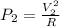

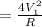
The ratio at which power is lost is
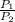
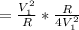
Here Resistance is constant
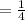
Hence the heat produced would be one fourth of the previous value