Question

6. The manufacturing of semiconductor chips produces 2% defective chips. Assume the chips are independent and that a lot contains 1000 chips. Approximate the probability that more than 25 chips are defective. [Hint: use normal approximation to binomial

Answer 1

Probability that more than 25 chips are defective is 0.1075.

Explanation:

We are given that the manufacturing of semiconductor chips produces 2% defective chips. Assume the chips are independent and that a lot contains 1000 chips.

The above situation can be represented through Binomial distribution;

`P(X=r) = \binom{n}{r}p^(r) (1-p)^(n-r) ; x = 0,1,2,3,.....`

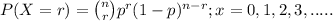
where, n = number of trials (samples) taken = 1000 chips

r = number of success = more than 25

p = probability of success which in our question is % of

defective chips, i.e; 2%

LET X = Number of chips that are defective

SO, X ~ Binom(n = 1000, p = 0.02)

Now, here we can't find the probability that more than 25 chips are defective using binomial distribution because the sample size is very large here (n > 30), so we will use Normal approximation to find the respective probability.

So, mean of binomial distribution = E(X) =
`n* p`

=
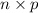
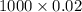`1000 * 0.02` = 20

Standard deviation of binomial distribution = S.D.(X) =
`√(n* p * (1-p))`

=
`√(1000 * 0.02 * 0.98 )`

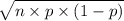
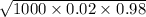
= 4.43

Let Y = Number of chips that are defective for normal approximation;

So, Y ~ Normal(
`\mu=20,\sigma = 4.43`)

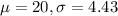The z-score probability distribution for normal distribution is given by;

Z =
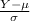`(Y-\mu)/(\sigma)` ~ N(0,1)

Now, probability that more than 25 chips are defective is given by = P(Y > 25) = P(Y > 25.5) --------------{using continuity correction}

P(Y > 25.5) = P(
`(Y-\mu)/(\sigma)` >
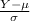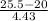`(25.5-20)/(4.43)` ) = P(Z > 1.24) = 1 - P(Z
`\leq` 1.24)

= 1 - 0.89255 = 0.1075

The above probability is calculated using z table by looking value of x = 1.24 in z-table.

Therefore, the probability that more than 25 chips are defective is 0.1075.