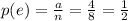Question

A spinner is divided into 8 section of equal size. The sections are numbered 1 through 8. Use this information to determine the probability of the needle landing on

Answer 1

1) 1/8

2) 1/2

Explanation:

1)

First of all, we notice that the spinner is divided into 8 sections of equal size.

So the number of sections is

n = 8

Secondly, we note that each section has the same size: this means that the probability of the spinner landing on each section is the same.

The probabilty of a certain event A to occur is given by

`p(A)=(a)/(n)`

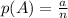
where

a is the number of successfull outcomes (in which A occurs)

n is the total number of possible outcomes

Here we want to find

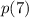`p(7)` = probability that the spinner lands on section 7

Here we have:

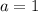`a=1` (only 1 outcome is successfull: the one in which the spinner lands on section 7)

`n=8`

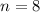
Therefore, the probability is

`p(7)=(1)/(8)`

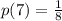
2)

Here we want to find the probability that the spinner lands on an even numbered section.

As before, the total number of possible outcomes his:

`n=8`

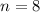
which corresponds to: 1, 2, 3, 4, 5, 6, 7, 8

The even-numbered sections are:

2, 4, 6, 8

So, the number of successfull outcomes is

`a=4`

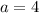
Because there are only 4 even-numbered sections.

Therefore, the probability that the spinner lands on an even numbered section is:

`p(e)=(a)/(n)=(4)/(8)=(1)/(2)`