Question

PR is tangent to clrcle Q at R and PS is tangent to circle Q at S. Find mZP.
​

Answer 1

Given:

It is given that PR is tangent to clrcle Q at R and PS is tangent to circle Q at S.

We need to determine the measure of ∠P

Measure of ∠P:

Since, the angles P and Q are circumscribed angles. And the angles add up to 180°

Thus, we have;

`\angle P+\angle Q=180^(\circ)`

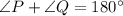
Substituting
`\angle P=x^(\circ)` and
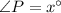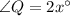`\angle Q=2x^(\circ)` in the above formula, we get;

`x^(\circ)+2x^(\circ)=180^(\circ)`

`3x^(\circ)=180^(\circ)`

`x=60^(\circ)`

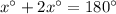
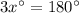
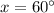
Thus, the value of x is 60°

The measure of ∠P = x = 60°

Hence, the measure of ∠P is 60°