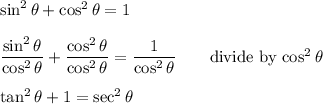Answer:
(a) sec²(θ) -tan²(θ) = 1
Explanation:
The identity relation between sec(θ) and tan(θ) is ...
tan²(θ) +1 = sec²(θ)
__
When tan²(θ) is subtracted from both sides of this equation, the result matches the first choice:
sec²(θ) -tan²(θ) = 1
_____
Additional comment
This is a variation of the "Pythagorean" relationship between sine and cosine. There is a similar relation between cot²(θ) and csc²(θ).