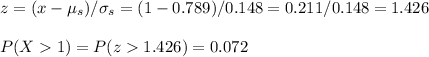Question

A roulette wheel in a casino has 38 slots. If you bet a dollar on a particular​ number, you'll win ​$30 if the ball ends up in that slot and​ $0 otherwise. Roulette wheels are calibrated so that each outcome is equally likely.

Answer 1

a) X=0 P(0)=0.9737

X=30 P(30)=0.0263

b) Mean: 0.789

SD: 4.801

c) P(X>1)=0.072

Step-by-step explanation:

The question is incomplete:

a) Let denote X your winnings when you play once. State the probability distribution of X.

b) You decide to play once a minute for a total of 1050 times. Find the mean and standard deviation.

c) Refer to (b). Using the Central Limit Theorem, find the probability that with this amount of roulette playing, your mean winnings is at least $1 (so, you don't lose money).

a) X has only two possible states: "0" and "30". The probability distribution for x is:

X=0 P(0)=37/38=0.9737

X=30 P(30)=1/38=0.0263

b) First, we calculate the mean and standard deviation of the population as:

`\mu=30*0.0263+0*0.9737=0.789\\\\\sigma=√(0.0263(30-0.798)^2+0.9737*(0-0.798)^2)=√(0.0263*852.76+0.9737*0.64)\\\\\sigma=√(23.05) =4.801`

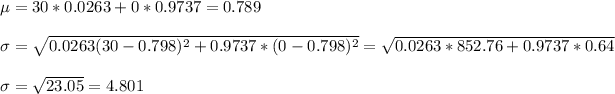
Then, the sampling distribution has these mean and standard deviation:

`\mu_s=\mu=0.789\\\\\sigma_s=\sigma/√(n)=4.801/√(1050)=4.801/32.404=0.148`

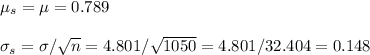
c) If we use the CLT, we can approximate this binomial distribution with a normal distribution to facilitate the calculations.

To calculate the probabilities of a outcome that is equal or bigger than $1, we first calculate the z-value:

`z=(x-\mu_s)/\sigma_s=(1-0.789)/0.148=0.211/0.148=1.426\\\\P(X>1)=P(z>1.426)=0.072`