Final answer:
The total momentum of the system of the two carts is 9.64 kg·m/s. The initial velocity of the first cart, when the second cart was still at rest, was also 4.6 m/s, as the total momentum of the system is conserved.
Step-by-step explanation:
To solve this problem, we will use the principle of conservation of momentum, which states that the total momentum of a system remains constant if no external forces are acting on it. Since the track is frictionless, we can assume no external forces act on the carts.
Part (a): Total Momentum of the System
The total momentum can be calculated as follows:
ptotal = pcart1 + pcart2
ptotal = (m1 × v1) + (m2 × v2)
ptotal =
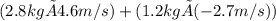
ptotal = 12.88 kg·m/s - 3.24 kg·m/s
ptotal = 9.64 kg·m/s
Part (b): Initial Velocity of the First Cart
Using the conservation of momentum before the second cart starts moving:
m1v1i + m2v2i = m1v1f + m2v2f
Since the second cart is initially at rest, v2i = 0, and:
v1i = (m1v1f + m2v2f)/m1
v1i =
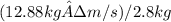
v1i = 4.6 m/s
Therefore, the velocity of the first cart when the second cart was still at rest was 4.6 m/s, the same as its velocity at the later time described in the problem because the total momentum of the system has not changed.