Answer:
The ratio of the rotational energy to the translational kinetic energy is 0.00618
Step-by-step explanation:
If m is the mass of the baseball and v its speed, then the translational kinetic energy is
Kt = 1/2 mv²
If I is its rotational inertia and ω is its angular speed, then the rotational kinetic energy is
Kr = 1/2 Iω²
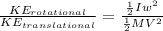
But the rotational inertia of a uniform sphere is I = 2mr²/5
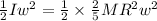
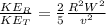
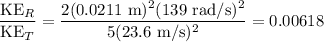
Therefore, the ratio of the rotational energy to the translational kinetic energy is 0.00618.