Question

Calculate the Fermi energy and the conductivity at room temperature for germanium containing 5×10^16 arsenic atoms per cubic centimeter. (Hint: Use the mobility of the electrons in the host material.)Use the mobility of the electrons in the host material.

Answer 1

The Fermi energy is 0.568 eV and the conductivity at room temperature is 31.24 (Ωcm)⁻¹

Step-by-step explanation:

Data given:

Nd = doping concentration = 5x10⁶/cm³

According the mass action law, the hole concentration is:

`P_(0) =(n_(i)^(2) )/(n_(0) ) ,n_(i)=2x10^(13) /cm^(3)`

`E_(f) =E_(i) +KTln((n_(D) )/(n_(i) ) ),K=8.61x10^(-19) ,KT=0.026eV`

`E_(i) =(E_(0) )/(2) =(0.63)/(2) =0.315eV\\E_(f)=0.315+0.203=0.568eV`

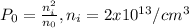
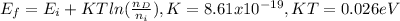
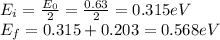
The conductivity of n-type of semi-conductor is equal to:

The mobility of Germanium is 3900 cm²/Vs

σ = 1.6x10⁻¹⁹ * 5x10¹⁶ * 3900 = 31.24 (Ωcm)⁻¹