Answer:
The probability that no calls will occur during the next ten minutes is 0.0907.
Explanation:
Poisson distribution:
Poisson distribution is a statistical distribution that helps to find out the number of events is likely occur in a specific time period.
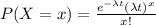
Given that,
Calls occur at an average rate of 1.2 every 5 minutes.
The average rate of call is
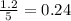 per minute.
per minute.
Here,
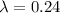 , t=10 and x=0
, t=10 and x=0
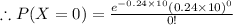
=0.0907
The probability that no calls will occur during the next ten minutes is 0.0907.