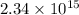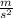Question

An electron passes through a point 2.83 cm 2.83 cm from a long straight wire as it moves at 35.5 % 35.5% of the speed of light perpendicularly toward the wire. At that moment a switch is flipped, causing a current of 17.7 A 17.7 A to flow in the wire. Find the magnitude of the electron's acceleration a a at that moment.

Answer 1

The magnitude of electron acceleration is
`2.34 * 10^(15)`
`(m)/(s^(2) )`

Step-by-step explanation:

Given:

Distance from the wire to the field point
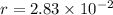`r = 2.83 * 10^(-2)` m

Speed of electron
`v = 35.5 \%c`

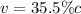
Current
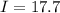`I = 17.7` A

For finding the acceleration,

First find the magnetic field due to wire,

`B = (\mu _(o)I )/(2\pi r )`

Where
`\mu_(o) = 4\pi * 10^(-7)`

`B = (4\pi * 10^(-7) * 17.7 )/(2\pi (2.83 * 10^(-2) ) )`

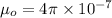
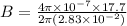
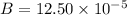`B = 12.50 * 10^(-5)` T

The magnetic force exerted on the electron passing through straight wire,

`F = qvB`

`F = 1.6 * 10^(-19) * 0.355 * 3 * 10^(8) * 12.50 * 10^(-5)`

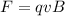
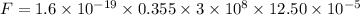
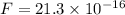`F = 21.3 * 10^(-16)` N

From the newton's second law

`F = ma`

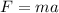
Where
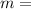`m =` mass of electron
`= 9.1 * 10^(-31)` kg

So acceleration is given by,

`a = (F)/(m)`

`a = (21.3 * 10^(-16) )/(9.1 * 10^(-31) )`

`a = 2.34 * 10^(15)`
`(m)/(s^(2) )`

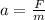
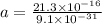
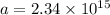
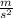
Therefore, the magnitude of electron acceleration is
`2.34 * 10^(15)`
`(m)/(s^(2) )`