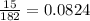Answer:
Required Probability in the lowest terms as fractions =
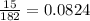
Explanation:
Step 1:-
Given Suzan has three red marbles, two green ones, five white ones, and two purple ones.
Total marbles = 3R+2G+5W+2P = 12
The number of exhaustive cases that the five marbles drawn from 12 marbles
n(S) =
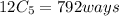
by using formula
 = 792
= 792
The number of favorable cases
She has drawn two red marbles from 3 red marbles, that is 3c₂ ways
she has drawn one marble drawn from 2 green marbles, that is 2c₁ ways
she has drawn one marble drawn from 5 white marbles, that is 5c₁ ways
she has drawn one marble drawn from 2 purple marbles, that is 2c₁ ways
The favorable cases are (n(E) = 3c₂ X 2c₁X5c₁X2c₁ = 60 ways
Required Probability =
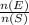
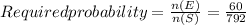
Required Probability in the lowest terms as fractions =