Question

Assume that the total revenue received from the sale of x items is given​ by, ​R(x)equals34 ln (4 x plus 5 )​, while the total cost to produce x items is ​C(x)equalsx divided by 2. Find the approximate number of items that should be manufactured so that​ profit, ​R(x)minus​C(x), is a maximum.

Answer 1

63 units

Explanation:

The profit function P(x) is given by the revenue function minus the cost function:

`P(x) = R(x) - C(x)\\P(x) = 34ln(x+5)-(x)/(2)`

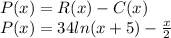
The number of units sold 'x' for which the derivate of the profit function is zero, is the number of units that maximizes profit:

`P(x) = 34ln(x+5)-(x)/(2)\\P'(x) =0= (34)/(x+5)-(1)/(2)\\x+5=68\\x=63\ units`

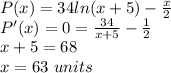
The number of units that should be manufactured so that​ profit is maximum is 63 units.